例えば、あのCGや動画はどうやって創られているのか。AIはどうやって思考や分析をしているのか。ロケットはなぜ飛ぶのか――どれも専門性が高すぎて「そんな難しいこと分かるわけない」「自分には縁のない話だよ」と思う人も多いでしょう。
しかし、「それぞれ異なる分野のように見えて、実は共通して用いられているのが数学なんです。あっ、でも難しい計算なんてできなくてもノープロブレム! 数学がどこにどう使われているのか知っているだけでも、理工系、情報系の学びがめちゃくちゃ楽しくなりますよ!」と軽いノリで語るのは、高橋隆史先生。
いや、でもそう言われても「ほんまかいな!?」って思っちゃいますよね。なら、実際にどう楽しいのか、先生に直接教えてもらうのが1番! ということで、疑い半分・期待半分でお話を伺ってきました!
今回のなかのヒト



高橋
高橋 隆史准教授
数理・情報科学課程
三角関数で絵が描けちゃう!?

インタビュアー
先生! さっそくですが、数学の何を知ると学びが楽しくなるんでしょうか。

高橋
おっと、いきなりド直球ですね。うーん、それについては「数学とは」みたいな堅苦しい話を100回聞くより、まずは1度、実際に数学で「遊んで」みるのがてっとり早いですよ!

インタビュアー
「遊ぶ」? 「学ぶ」じゃなくて?

高橋
そうです。ちょっとこれを見てもらえますか?
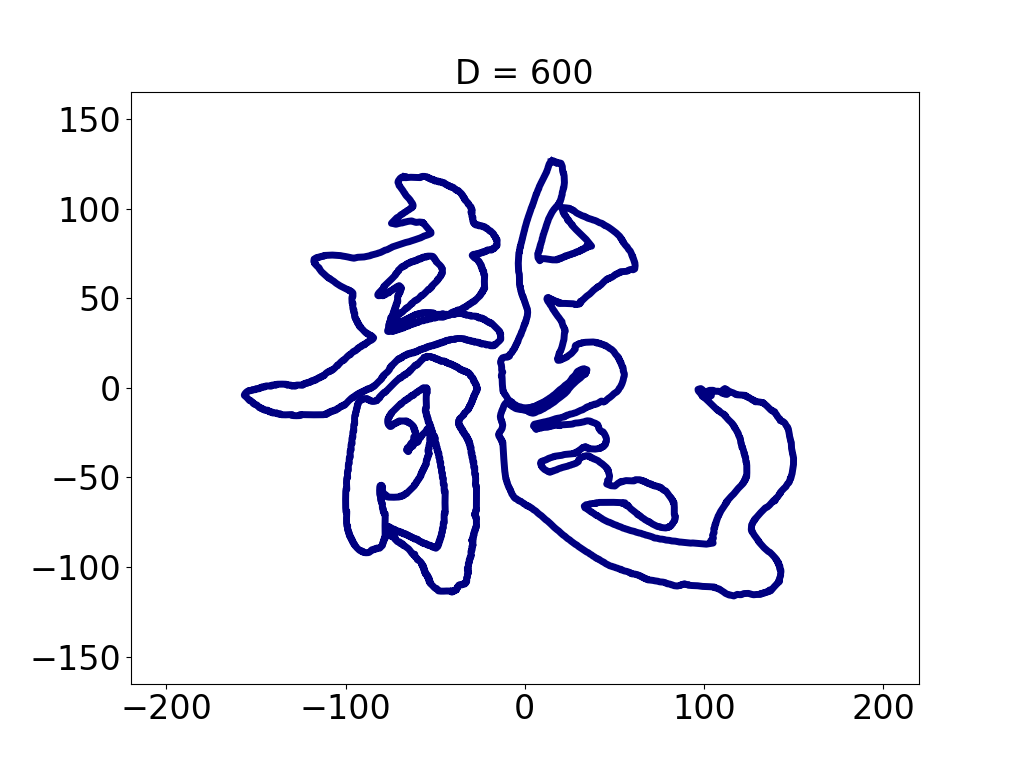

インタビュアー
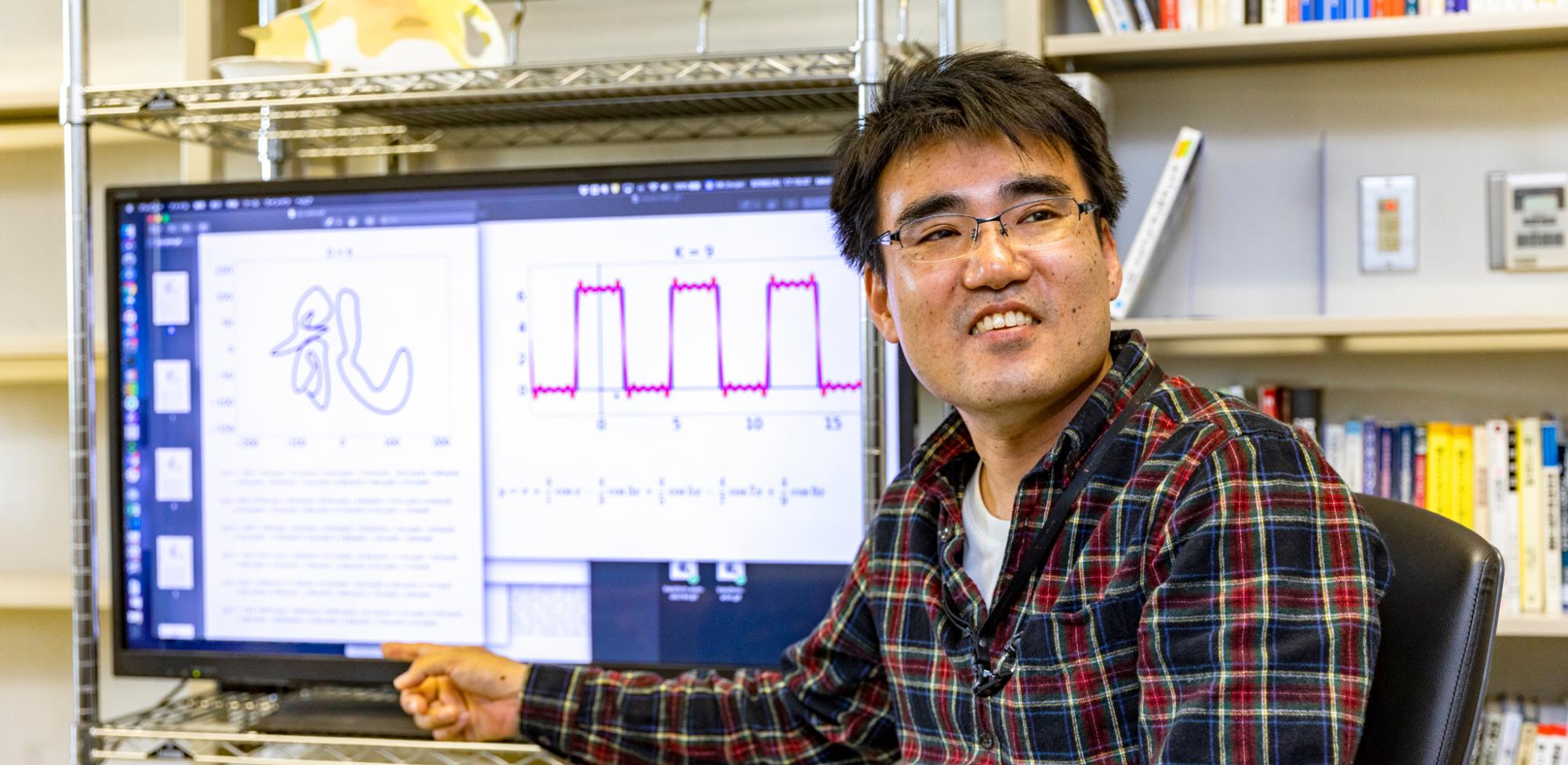
龍谷大学の「龍」という字の画像ですね。これが何か?

高橋
フフフ……字に見えますか? まあ見えますよね。でも実はこれ、三角関数の数式でできてるんです。

インタビュアー
?? すみません、ちょっと言ってる意味が分かんないです。

高橋
いやだから、数式なんです。厳密にいえば、三角関数を使って描いた曲線ですね。実際に数式そのものを示すと、こんなかんじ。本当はこの30倍の長さがあるんで、ここでは省略して短くしてみました♡


インタビュアー
ありがとうございました。では、今日はこのへんで失礼します……

高橋
待て待て待てーい(笑)! いや、ごめんごめん。分かりますよ、見た瞬間イヤになりますよね。でも安心してください。ここで式の中身を理解したり、計算したりする必要なんてないですから。要は、三角関数の数式で絵(字)が描けるんだってことだけでも分かれば大丈夫

インタビュアー
すみません、長い数式を見るとついめまいが……でもそこなんですよ。なんで三角関数で絵が描けちゃうんですか?

高橋
三角関数の基本は分かりますね? サイン(sin)、コサイン(cos)、タンジェント(tan)っていうあれです。あれを使ってグラフを書くことがあるじゃないですか? そこで、グラフの示す曲線が思いどおりの形になるように数式を作って、絵にしているだけなんですよ。だから、これは絵じゃなくてグラフなんです!


インタビュアー
えっ、三角関数って辺の長さや角度を求めたりするときに使うんじゃないんですか?

高橋
まあ基本はそうですけど、そんなふうに考えるから数学がつまんなくなるんですよ。「三角関数のグラフで絵が描けちゃう。なんだこれ!? おもしれーーーーっ!!」で十分なんです。実際、計算式の中身なんて分からなくても、おもしろいでしょ?

インタビュアー
たしかに。学校でグラフを書かされてるときは、正直、これの何が楽しいのかって思ってました。でも、こんなことができたらなんだか楽しそうです!もっと複雑な絵も描けるんですか!?

高橋
もちろんです。これを見てください。

高橋
画像(グラフ)の上の「D」の値が大きくなればなるほど、「龍」の画像も複雑になっているのが分かりますか?この D は、式に出てくるsinやcosの数のことです。それと同時に、下に表示された数式も長くなっているでしょう?

インタビュアー
お……、お? おおーーーーっっ!! うわすごい、単なる円が龍の字になりました!! 細かいことはともかく、式が長くなる=線の変化が細かくなる、つまり数式を複雑化すれば、それだけ絵も「描きこんだ」ものにできるっていうことですか?

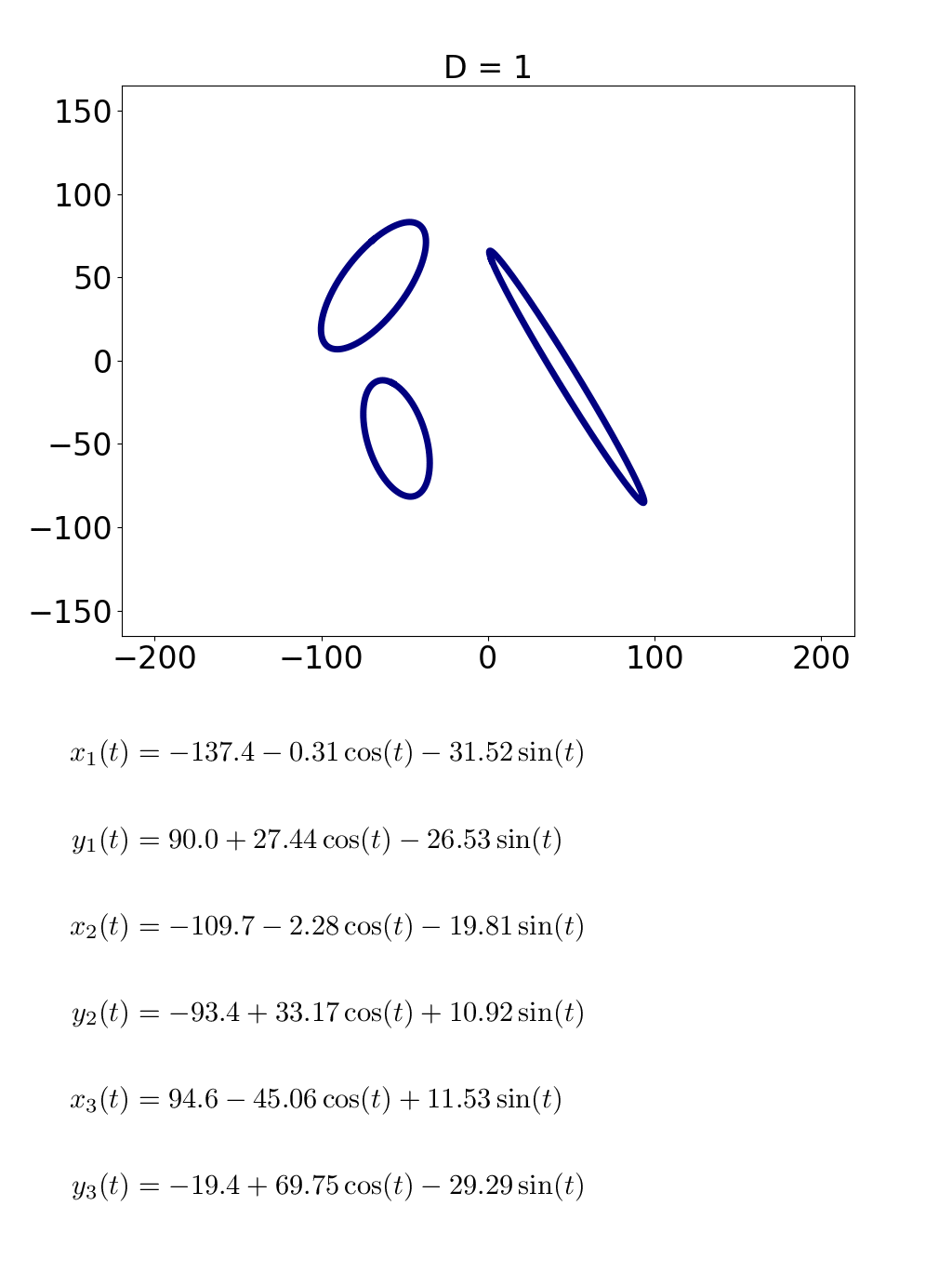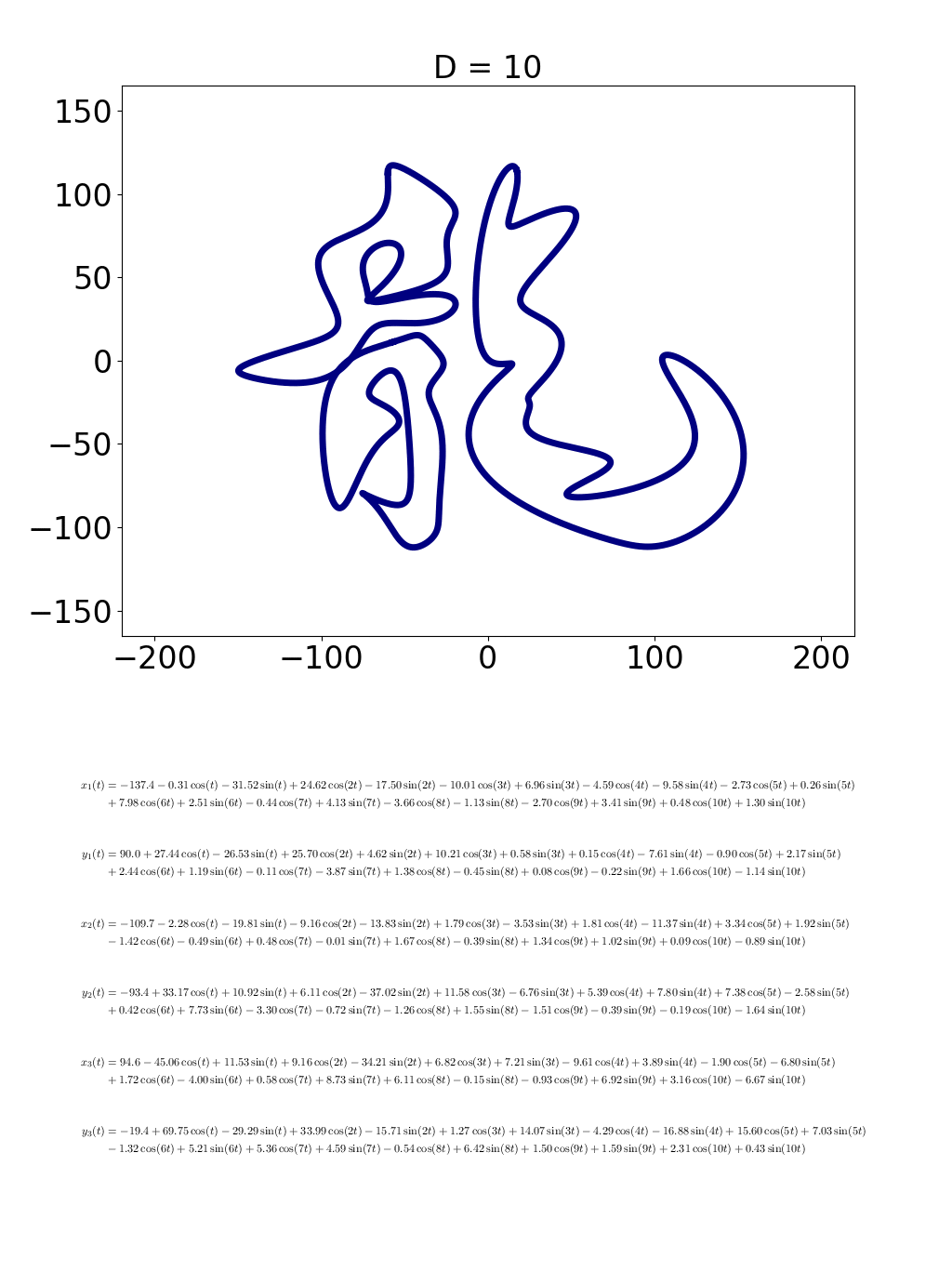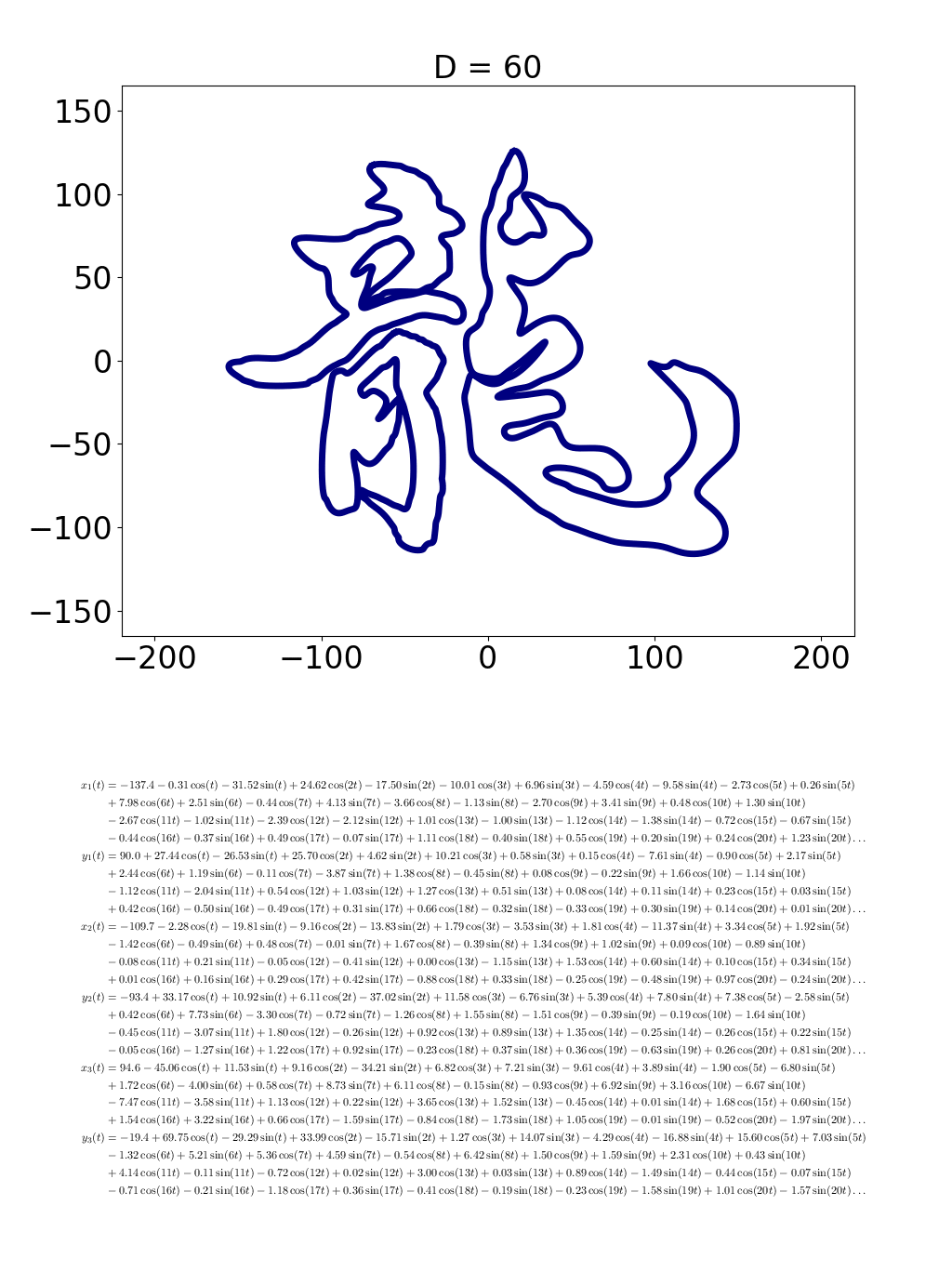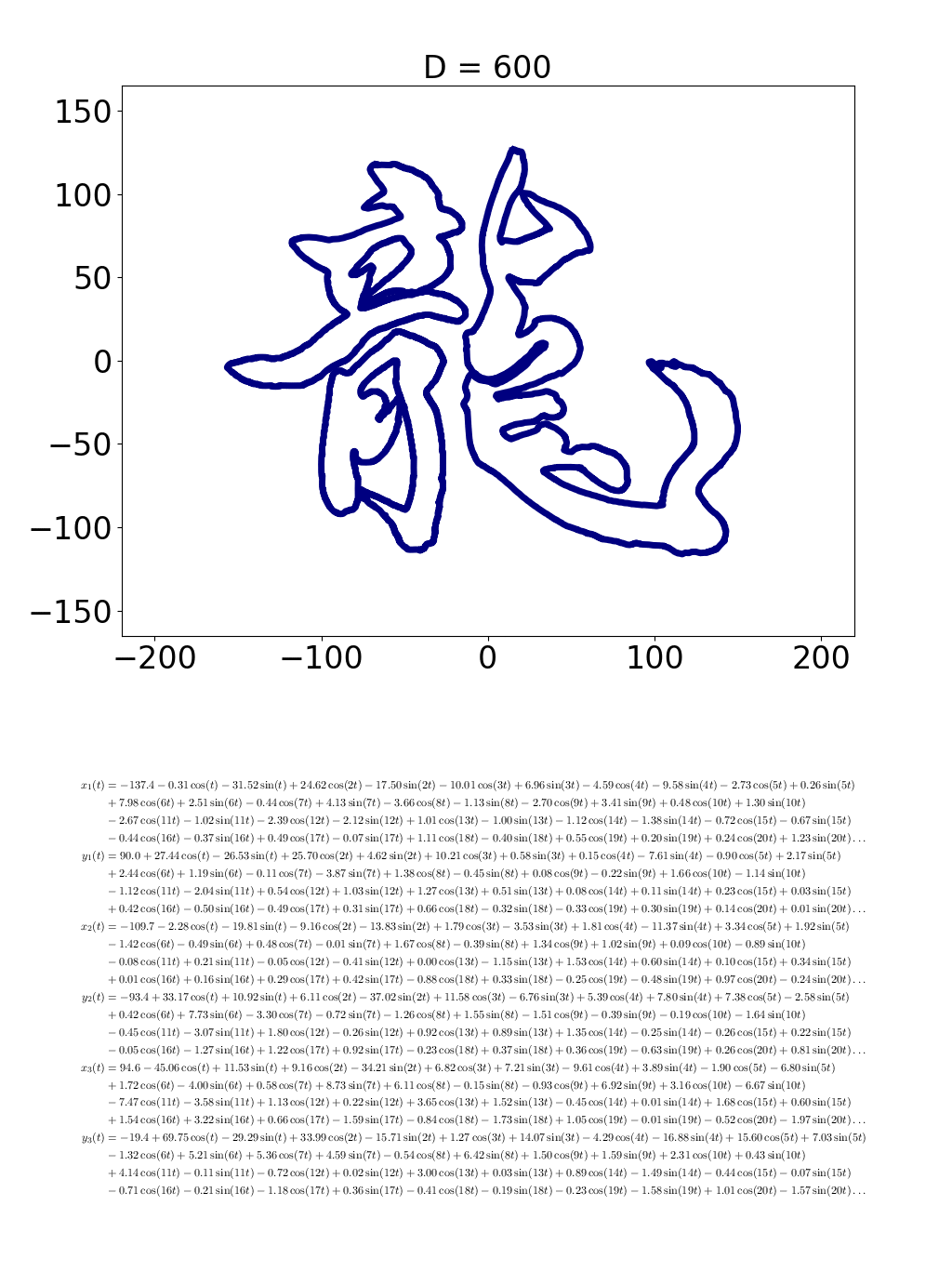
高橋
そういうことです。「D=1」のとき、つまり数式が単純なときは3つの楕円があるだけです。これが「龍」の字を構成するパーツ、「立」とか「月」とかの原型ですね。
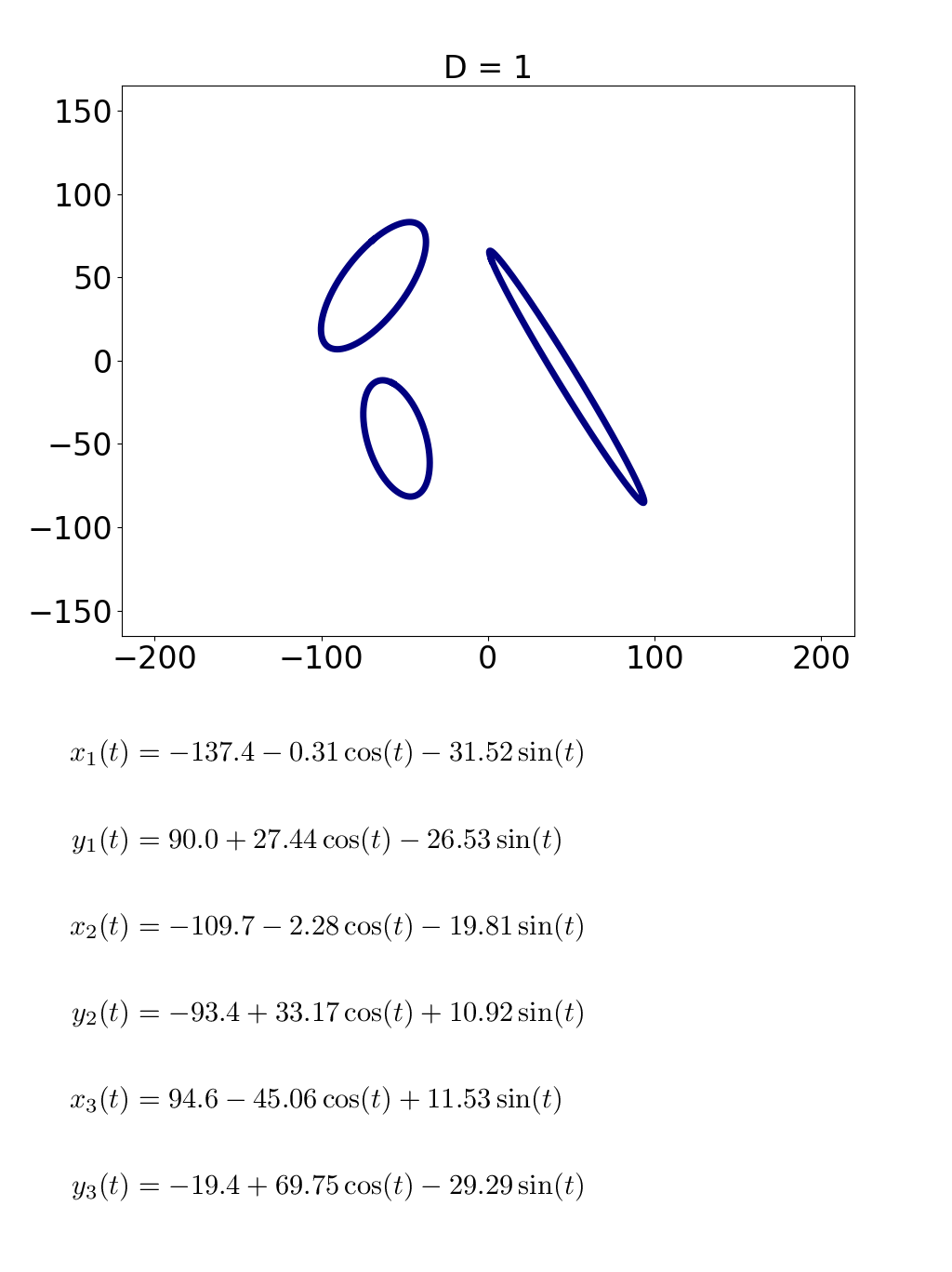

高橋
これが「D=2」になるとこうなります。形にちょっと変化が出て、式も少し長くなりましたね。
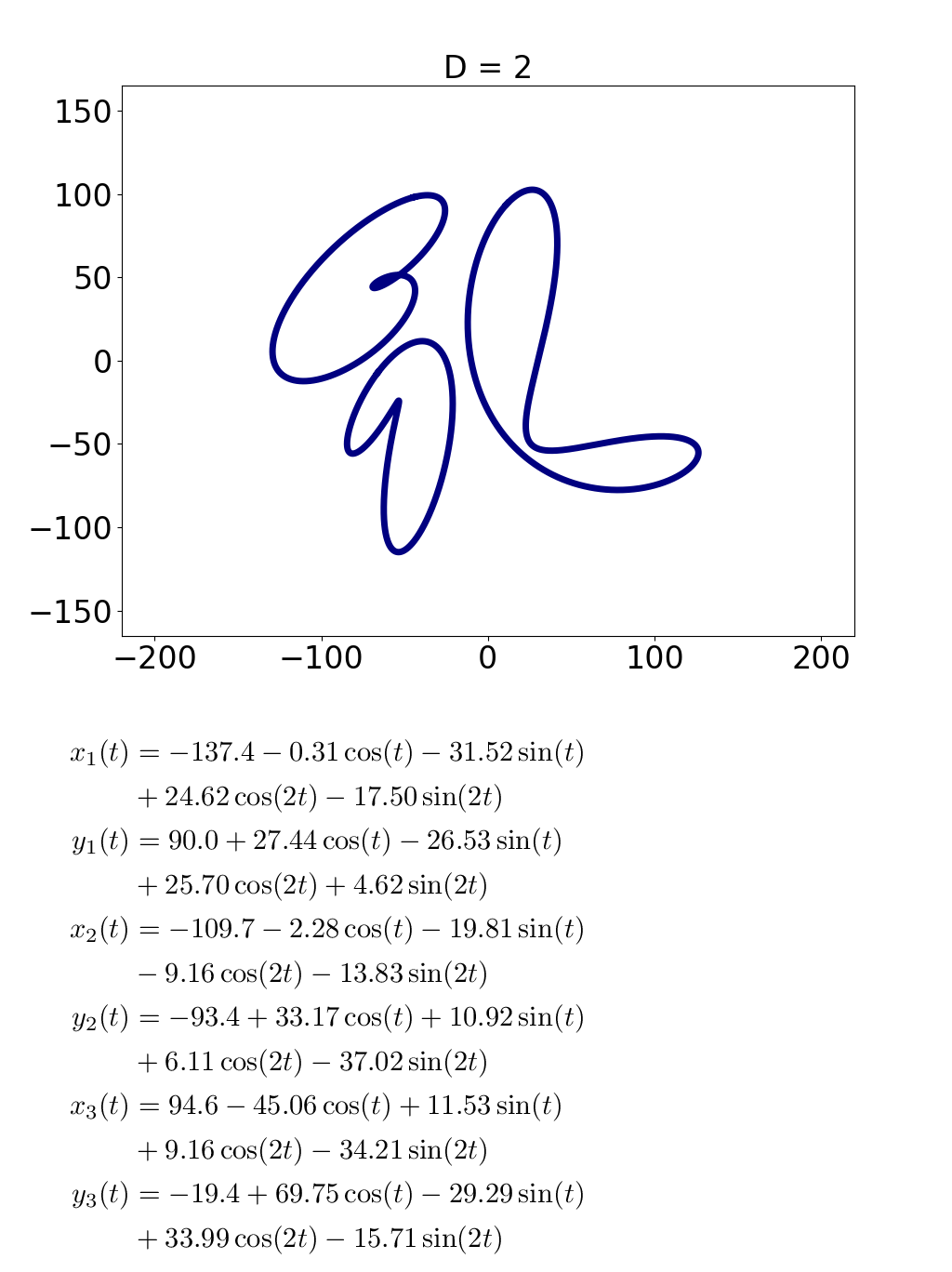

高橋
さらに、D=20になるとこうです。
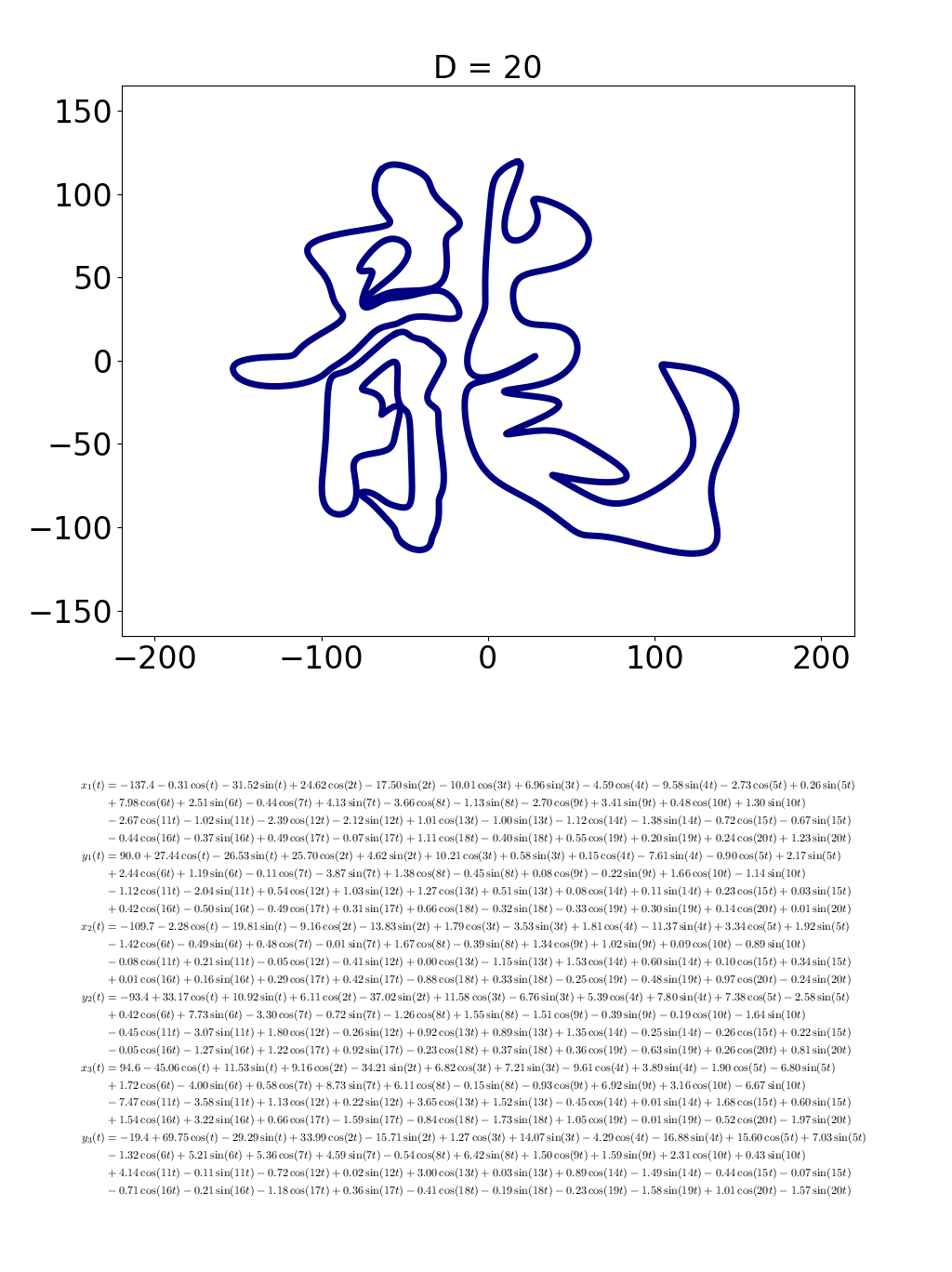

インタビュアー
おおおっ! ここまでくると、「龍」の文字だと分かるようになってきました!

高橋
ね、おもしろいでしょう? 繰り返しますが、これ、ぜんぶほんとはグラフなんですよ。こうした「グラフのもとになった数式を変化させて絵の形を変える」行為の途中経過をつないでいけば、こんなアニメーションもできちゃいますよ。「龍の字を本学のロゴに「変身」させてみましょう。


インタビュアー
うわっ、字が絵に変わった!! こんなことまでできるなんて!!
画像も音声も、この世のあらゆるものは、
三角関数で数式化できる!?

インタビュアー
僕もやってみたいなあ……でも、こんな複雑な計算なんてできないです。先生くらいの専門性がないと無理ですよ。

高橋
いやいやいやいや! 私だって、こんな長い計算するのなんてまっぴらです。だってめんどくさいじゃないですか(笑)。そういうめんどくさいことは、コンピュータにやらせとけばいいんです。実は大学の理工系分野では、みなさんの想像以上に数学を道具として「使う」んですけど、ほとんど手計算なんてしません。だから私たちは、「なぜそうなるのか」という原理さえ分かっておけば、なんとかなります。

インタビュアー
そう考えると、少しハードルが下がったように感じて安心できます。

高橋
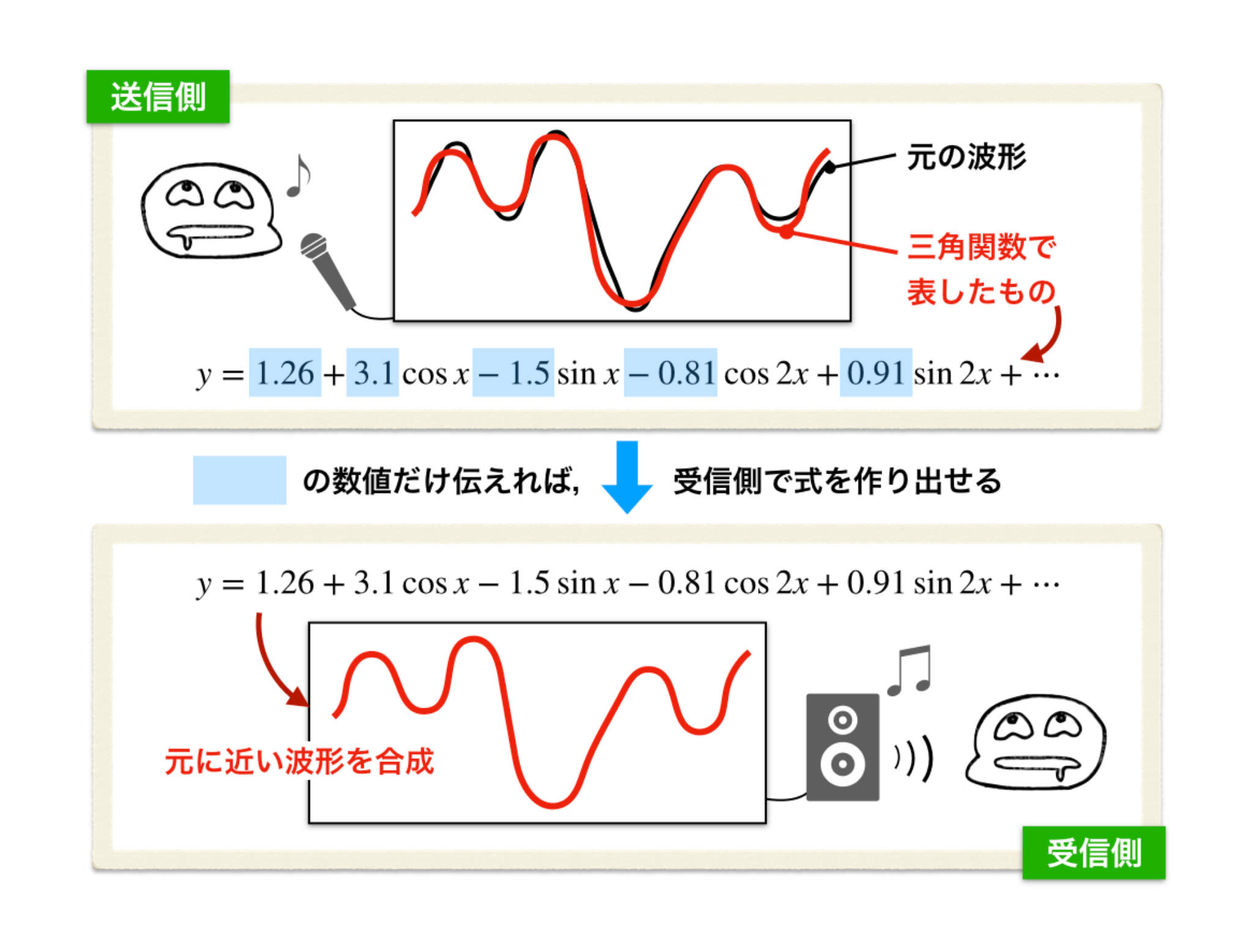
ま、原理を分かるためには、やっぱりがんばって手計算する経験をしておくのも大事なんですけどね。少しだけ数学的な原理の話をすると、このように曲線を三角関数の式で表すことを、「フーリエ変換」と呼びます。絵を数式に“翻訳”していると考えてもいいでしょう。

高橋
今回の「龍」の字は、うちの研究室の学生が筆と墨で書いてくれたものを、スキャンして画像としてパソコンに取りこみました。それを画像処理してフーリエ変換しているのですが、このあたりもコンピュータでちょろっとプログラムを書けばすぐできます。

インタビュアー
えっ? ということは、原理的にはどんなものでも数式化できるんですか!?

高橋
ほほう、ついに気付いてしまいましたね……。そうです。実は、この世の曲線で表せるものは、すべて数式化することが可能です。気付かなければ良かったものを……キミのような勘のいい子は嫌いだよ……

インタビュアー
けっ、消される!!

高橋
まあそれは冗談として(笑)、こういう数学が実社会で役立ってる例をあげるなら、電話や音楽を考えるのが分かりやすいでしょう。そもそも、「音」って何ですか?何でできている、というか。

インタビュアー
音波……ですか?

高橋
そうですね。音っていうのは、空気の振動による「波」ですね。「音の大きさ」はこの波の振れ幅に対応してます。それから、「音の高さ(音程)」は、波の振動の数(1秒間に何回方向を変えるか)によって決まります。「周波数」って語を聞いたことあるかもしれませんが、低い音は振動数が小さく(周波数が低く)、高い音は振動数が大きい(周波数が高い)のです。で、数学や物理の世界で波とか振動とか言うと…

インタビュアー
波……振動……

高橋
ほら、波なみ~って感じの数式ですよ

インタビュアー
あっ、sinとかcosとか!!

高橋
いい感じですね~。そうです。三角関数ですね。音波を表す波の形も、グラフで表せるということです。じゃあ、これを数式化し、数値をいじって波の形を変えると?
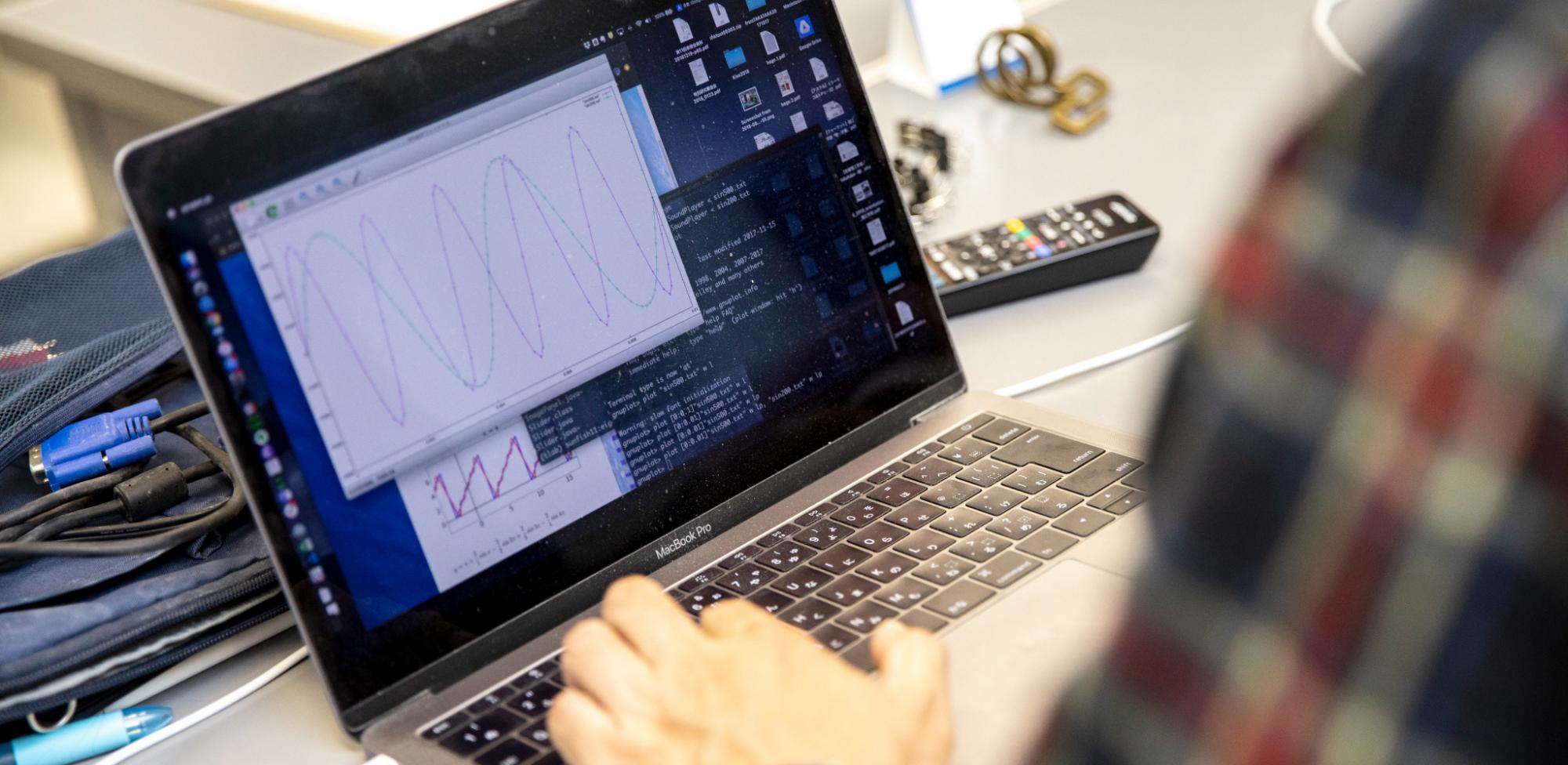

インタビュアー
違う音になる!!

高橋
そーーーーーなんです!! 音量を上げたり、ミュートやエコーをかけたり、重低音を効かせたりするのもそう。オーディオ機器で、棒グラフみたいなのが上下する演出効果を見たことはありませんか? あれは、音をいろいろな高さの成分(=いろいろな周波数の三角関数)に分解して数式化したときに、どの成分が強いかを視覚化したものなんですよ。あと、シンセサイザーってあるでしょう? あれの仕組みも、機械の中で数式を変化させて音を変えているんですね。

インタビュアー
すごいすごい!「中」でそんなことが起こっていたなんて! めっちゃおもしろいです!

高橋
ここまで話すともう分かってきたかと思いますが、実は、私たちがパソコンや携帯電話で聞いてる音は、フーリエ変換みたいな方法を使って数式から作り出されたものなんです。音を数式に変換し、数式から音に再変換して出力する、みたいな。アプリで音を加工するのも、原理としてはそうやって数式をいじってるだけなんですよ。電話はできるだけ音質を変えずに再現することが大事ですが、お遊び感覚で考えれば、あなたの声をシブいバリトンボイスや、萌えるアニメ声に変換して再生することは、理論上可能なんです。

インタビュアー
まじかーーーーー!! いや、数学の奥深さというか、おもしろさがだんだん分かってきました!
あっ、だとすると、音楽データの容量が大きくて「重い」とか言ったり、音質が良かったりするのって……

高橋
ビンゴです! 音や画像のようなデータの容量を小さくする処理を「データ圧縮」っていうんですが、つまりそれは数式を短くしてるんですね。容量の重い軽いや音質って、要は三角関数みたいなもので表わした数式の長さと比例していて、短い数式だと容量が小さくて「軽い」かわりに質は落ちます。長い数式にすれば「重い」けど質が良くなる、っていうカラクリです。

インタビュアー
え、じゃあ画像の場合も同じですか?

高橋
ご名答! 画像も音と同じで、つまるところ「波」と考えることができるんです。縦横に広がった波です。大きな波が大まかな形を表して、細かい波が細かい形を表す、というとイメージできるでしょうか。この波の形もやはりすべて数式化できます。圧縮して画像データの容量を軽くするということは、簡単に言うと、数式を短くすることなんです。細かい波を表す式を切り捨てちゃうわけです。


高橋
いやあ、それにしても、気付かなければ良かったものを……

インタビュアー
真剣に怖いんで、やめてもらっていいですか……
実は人気のあのキャラも!?
知らないうちに数式に熱狂していた私たち

インタビュアー
形あるものを数式化する「フーリエ変換」で、絵や音を作ったり、変化させたりできる……あっ、ということは、動画投稿サイトの「歌わせてみた」なんかでおなじみの、「ネギに縁のある、青髪ツインテールのお嬢さん」もそういうことですね!?

高橋
だんだんヒートアップしてきましたね!! 大人の事情も配慮できていてすばらしいです。そう、彼女らの歌声は、フーリエ変換で数式化されたものを加工した産物です。また、彼女らのライブで流される映像、つまりお嬢さんたちが歌い踊る動画も同じ技術が使われています。極論すれば、視覚的にも聴覚的にもすべて三角関数みたいな数式で構成されているということであり、私たちは数式に声援を送っているのも同然なのです!!

インタビュアー
い、いやちょっと、それは極端では……あっ、でも数式(数学)で、こんなにも人の心を動かすことだってできるんだ、って考えることもできますよね。

高橋
おお~、いいことを言いますね! そのとおりです。数学や、数学でできることを楽しいと感じられること、それがスタートですからね。今日お話しした三角関数やフーリエ変換は、電気、電波、地震など、波・振動が関係するあらゆるものを対象にできます。もっと話を広げると、高校数学で学ぶベクトルも、嫌いなひと多いかもしれませんが、ゲームなんかの3DのCGとか、VRやARとか、そういうところでたくさん使われてます。高橋の専門はAIとか機械学習という分野なんですが、微分積分とか確率統計とか超役立ちます。
筋トレばっかじゃつまらない!
大学からの数学で“その先”が見える!

インタビュアー
いやあ、楽しかった! 数学の見方が変わった気がします。めちゃくちゃおもしろいですね!

高橋
おっ、気付いてきましたね!? 数学って、手段であって目的じゃない。「道具」なんですよ。あくまで何かやりたいことがあって、そこに数学をどう使うのかっていう発想です。それが楽しいっていうか、そうじゃないと楽しくないと思いませんか?何かを計算して答えが合っていればそれだけで楽しい、っていう人もいるにはいますが、僕には無理です(笑)。

高橋
高校までの数学って、いわば「使う」ための基本を習っているようなもので、大学からの数学が実は本番、醍醐味と言っていいかもしれません。先ほども言いましたが、計算そのものなんてぜんぶコンピュータにやらせちゃいますし。


インタビュアー
つまり、高校までの数学は筋トレみたいなものだけど、大学からは試合にガンガン出られるぜ、みたいな?

高橋
そうそう。筋トレってキツいし、できればやりたくない。じゃあなぜ人は筋トレをするのか。筋力をつけること自体が楽しいっていう人もいるけど、たいていは、結果として試合で活躍したいとか、腹筋をシックスパックにしてモテたいとか、そっちが目的じゃないですか。

インタビュアー
はい、モテたいです!キャーキャー言われたいです!

高橋
高校までの数学でつまらなさや苦手意識を抱いちゃう人って、要はこの筋トレの時点でギブアップしてる面があるんですよね。「鍛えるばっかでつまんねー!」って。でもそれは根性がないからじゃなくて、その先を知らないからだと思うんです。そう考えるともったいないですよね。試合で大活躍できるかもしれないし、モテモテになれるかもしれないのに。

インタビュアー
ホントそうですよね。いやぁ~、よく分かりました!数学の楽しさもたくさん知ることができましたし。これで僕も明日からモテそうな気がします!

高橋
最後のやつはまた別問題です(キッパリ)。


